R para el análisis de datos

Kevin Carrasco

Sociología - UAH

1er Sem 2024

R-data-analisis.netlify.com

Sesión 8: Regresión lineal y valores predichos

1 / 28

Sesión 8

Repaso sesión anterior

Valores predichos

2 / 28

Asociación: covarianza / correlación

¿Se relaciona la variación de una variable, con la variación de otra variable?

3 / 28

Pero ojo, correlación no implica causalidad

4 / 28

¿Qué es la regresión lineal?5 / 28

¿Qué es la regresión lineal?

Es un modelo estadístico que se usa para:
- Conocer: La relación de una variable dependiente de acuerdo a una/otras independiente(s)
- Predecir: Estimar el valor de una variable dependiente de acuerdo al valor de otras
- Inferir: si estas relaciones son estadísticamente significativas

5 / 28

¿Qué es la regresión lineal?Dos tipos de regresión:Regresión lineal simple (una variable independiente)
Regresión lineal múltiple (más de una variable independiente)

6 / 28

Ejemplo
##   Educacion Ingreso
## 1         1     250
## 2         2     200
## 3         3     250
## 4         4     300
## 5         5     400
## 6         6     350
## 7         7     400
## 8         8     350
7 / 28

Ejemplo

8 / 28

Ejemplo

9 / 28

La recta de regresión

$\hat{Y} = b_{0} + b_{1} X$

Donde

$\hat{Y}$ es el valor estimado de $Y$
$b_{0}$ es el intercepto de la recta (el valor de Y cuando X es 0)
$b_{1}$ es el coeficiente de regresión, que nos dice cuánto aumenta Y por cada punto que aumenta X

10 / 28

Estimación de los coeficientes de la ecuación:

$b_{1} = \frac{C o v (X Y)}{V a r X}$

$b_{1} = \frac{\frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{n - 1}}{\frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (x_{i} - \bar{x})}{n - 1}}$

Y simplificando

$b_{1} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (x_{i} - \bar{x})}$

11 / 28

Pero este es un curso de R, así que:

## 
## Call:
## lm(formula = Ingreso ~ Educacion, data = data)
## 
## Coefficients:
## (Intercept)    Educacion  
##         200           25

12 / 28

Estimación de los coeficientes de la ecuación:

$\bar{Y} = b_{0} + b_{1} \bar{X}$ Reemplazando:

$\bar{Y} = b_{0} + 25 \bar{X}$

Despejando el valor de $b_{0}$

$b_{0} = 200 - 0 \bar{X}$

13 / 28

Ejemplo

Por cada unidad que aumenta educación, ingreso aumenta en 25 unidades

14 / 28

Varianza explicada¿Qué porcentaje de la varianza de Y logramos explicar con X?
15 / 28

Varianza explicada¿Qué porcentaje de la varianza de Y logramos explicar con X?
R2 = Porcentaje de la variación de Y puede ser asociado a la variación de X
15 / 28

Ejemplo

El ajuste del modelo a los datos se relaciona con la proporción de residuos generados por el modelo respecto de la varianza total de Y (R2)

16 / 28

Inferencia estadística¿Cómo sabemos si b1b1 es estadísticamente significativo?
17 / 28

Inferencia estadística

¿Cómo sabemos si $b_{1}$ es estadísticamente significativo?
¿Nuestros datos se pueden extrapolar a la población?

17 / 28

Inferencia estadística

Según criterios muestrales:
- Distribución normal
- Desviación estándar
Error estándar

18 / 28

 
Model 1

(Intercept)
200.00**

(35.57)

Educacion
25.00*

(7.04)

R2
0.68

Adj. R2
0.62

Num. obs.
8

***p < 0.001; **p < 0.01; *p < 0.05

19 / 28

	Model 1
(Intercept)	200.00^**
	(35.57)
Educacion	25.00^*
	(7.04)
R²	0.68
Adj. R²	0.62
Num. obs.	8
^*p < 0.001; ^p < 0.01; ^*p < 0.05

 
Model 1

(Intercept)
106.12*

(33.92)

Educacion
7.07

(6.57)

edad
5.48*

(1.56)

R2
0.91

Adj. R2
0.87

Num. obs.
8

***p < 0.001; **p < 0.01; *p < 0.05

20 / 28

	Model 1
(Intercept)	106.12^*
	(33.92)
Educacion	7.07
	(6.57)
edad	5.48^*
	(1.56)
R²	0.91
Adj. R²	0.87
Num. obs.	8
^*p < 0.001; ^p < 0.01; ^*p < 0.05

Parcialización

21 / 28

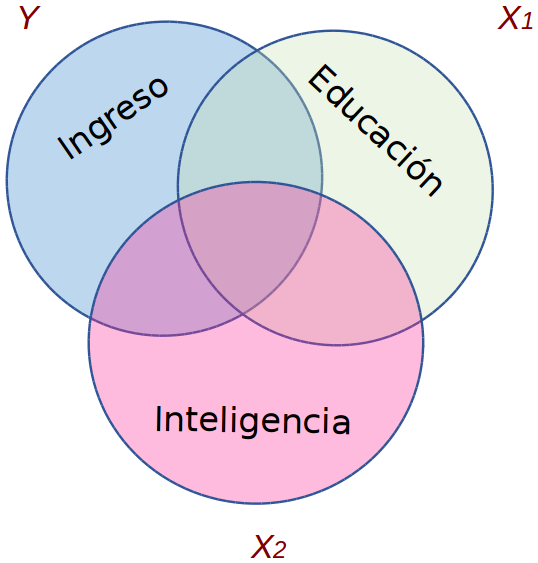
¿y la interpretación para variables categóricas?

	Model 1
Intercepto	233.33^***
	(23.57)
Educación media	116.67^*
	(37.27)
Educación superior	133.33^*
	(33.33)
R²	0.78
Adj. R²	0.70
Num. obs.	8
^*p < 0.001; ^p < 0.01; ^*p < 0.05

22 / 28

¿y la interpretación para variables categóricas?

	Model 1
Intercepto	233.33^***
	(23.57)
Educación media	116.67^*
	(37.27)
Educación superior	133.33^*
	(33.33)
R²	0.78
Adj. R²	0.70
Num. obs.	8
^*p < 0.001; ^p < 0.01; ^*p < 0.05

Las personas que tienen educación media ganan $116mil más en comparación con quienes tienen educación básica, efecto que es estadísticamente significativo (p<0.01)

22 / 28

Sesión 7

Repaso sesión anterior

Valores predichos

23 / 28

¿Cómo podemos predecir el valor esperado de una variable para una persona en particular?

	Model 1
Intercepto	233.33^***
	(23.57)
Educación media	116.67^*
	(37.27)
Educación superior	133.33^*
	(33.33)
R²	0.78
Adj. R²	0.70
Num. obs.	8
^*p < 0.001; ^p < 0.01; ^*p < 0.05

$\bar{Y} = b_{0} + b_{1} \bar{X}$

Reemplazando:

$\bar{Y} = 233 + b_{1} \bar{X}$

¿Si una persona tuviera un nivel de educación superior?

$\bar{Y} = 233 + 133$ $\bar{Y} = 366$

24 / 28

Graficando

25 / 28

Variables numéricas

Model 1

(Intercept)
96.44*

(33.14)

edad
6.78***

(0.99)

R2
0.89

Adj. R2
0.87

Num. obs.
8

***p < 0.001; **p < 0.01; *p < 0.05

26 / 28

	Model 1
(Intercept)	96.44^*
	(33.14)
edad	6.78^***
	(0.99)
R²	0.89
Adj. R²	0.87
Num. obs.	8
^*p < 0.001; ^p < 0.01; ^*p < 0.05

$\bar{Y} = b_{0} + b_{1} \bar{X}$

Reemplazando:

$\bar{Y} = 96.44 + b_{1} * 6, 78$

¿Una persona de edad 40?

$\bar{Y} = 96, 44 + 40 * 6, 78$ $\bar{Y} = 367.64$

27 / 28

R para el análisis de datos

Kevin Carrasco

Sociología - UAH

1er Sem 2024

R-data-analisis.netlify.com

Sesión 6: Índices y escalas

28 / 28

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Restart the presentation timer

?, h

Toggle this help